A mathematician named Klein
Thought the Möbius band was divine.
Said he: “If you glue
The edges of two,
You’ll get a weird bottle like mine.”
— Leo Moser, mathematician

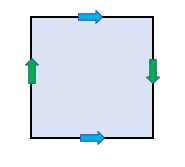
A Klein bottle contains many Möbius bands. In the glued rectangle, any band that spans the rectangle horizontally, crossing the two green edges, is a Möbius band. This is even true of bands that cross the blue edge, winding around the tube any number of times.

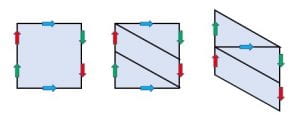
Recall that a Möbius band contains a single edge. A Klein bottle is made of two Möbius bands whose edges are glued together.¹ The figure below shows why. The left figure depicts a Klein bottle. The middle figure partitions the Klein bottle by a pair of parallel diagonals. To obtain the right figure, we detach the lower-left triangle from the middle figure and move it to the top, aligning the blue arrows. Each of the two resulting parallelograms is a Möbius band.

The following program shows two Möbius bands glued together to form the Klein bottle. Rendering one of the bands translucent helps us see ‘into’ the Klein bottle. I qualify ‘into’ because the Klein bottle has no interior or exterior; like the Möbius band, it is a one-sided surface. It is also non-orientable because paths along a Mobius band reverse orientation.

A Klein bottle