In the following program, earth simply rotates on its own axis.

Rotating earth

The code renders a fairly realistic rotating earth endowed with an equator. Our ziggurat programs have (hopefully) prepared us to take in the rotation behavior at a glance, but the texture and the red equatorial circle are new.

function createEarth(radius=2, rps, earthTexture) {
    let geom = new THREE.SphereGeometry(radius, 48, 48);
    let texture = getTexture(earthTexture);
    let matArgs = {map: texture,  specular: 0xFF9999, shininess: 10};
    let mat = new THREE.MeshPhongMaterial(matArgs);
    let earth = new THREE.Mesh(geom, mat);
    // equator
    let eqargs = {color: 0xff0000};
    let eps = 0.001;
    let equator = createCircle(radius + eps, eqargs);
    earth.add(equator);
    // behavior
    earth.rps = rps;
    earth.update = makeSpin(1);
    subject.register(earth);
    return earth;
}

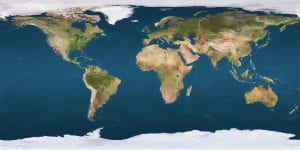
A texture is an image that gets mapped to a surface. Here’s the image we use:

To apply this image to the surface of a sphere, we use a default mapping while ensuring that the image’s edges get clamped to the edges of the sphere’s mesh, both horizontally and vertically. (Being a closed surface, a sphere has no edges, but the mesh used to represent the sphere does have edges.) To obtain the texture, we load it from an image file named src.

function getTexture(src) {
    let texture = new THREE.TextureLoader().load(src);
    texture.wrapS = THREE.ClampToEdgeWrapping;
    texture.wrapT = THREE.ClampToEdgeWrapping;
    return texture;
}

The equator is represented by a red circle that hovers slightly above the actual equator. We build the equator by calling this function:

function createCircle(radius, matargs={}) {
    let mat = new THREE.LineBasicMaterial(matargs);
    let geom = new THREE.CircleGeometry(radius, 48);
    geom.vertices.shift();  // get rid of center vertex
    let circle = new THREE.LineLoop(geom, mat);
    circle.rotation.x = Math.PI / 2;
    return circle;
}

The circle’s geometry is built from the call to CircleGeometry (line 3) which returns the geometry of a filled n-sided regular polygon. This geometry contains n+1 vertices: the first vertex lies at the center of the polygon, and the remaining ones are the polygon’s n vertices. To turn this into a cycle of n vertices approximating a circle, we excise the first vertex (line 4) and build a (closed) loop on the resulting geometry. Lastly, we rotate this loop from the xy-plane into the xz-plane in which our not-yet-tilted earth’s equator lies.