Transformations of the complex plane

The following program depicts transformations of the complex plane. The plane is represented by the blue disk containing a few smaller disks. The transformation is represented by the translucent disk suspended above it. As you change the abs slider, the transformation expands or contracts, and as you change the arg slider, it rotates around the origin.

The red axis is the real axis and the green axis is the imaginary axis. Numbers in the complex plane can be expressed in Cartesian coordinates as $x+iy$ . Here $x$ is the real part of the complex number, and $y$ is the imaginary part. The symbol $i$ represents the square root of -1, that is, $i=\sqrt{-1}$ , so that $i\times i=\sqrt {-1}\times \sqrt{-1}=-1$ . Complex numbers are often regarded as points in the complex plane.

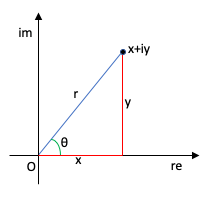
Complex numbers may also be written in polar coordinates $P=(r,\theta)$ . Here $r$ is point $P$ ‘s distance from the origin $O$ (that is, $r=|\overline{OP}|$ ), and $\theta$ is the angle between the line $\overline{OP}$ and the real axis. Where $z$ is a complex number, $r$ is called the absolute value or modulus of $z$ , denoted $|z|$ , and $\theta$ is called the argument of $z$ , denoted (for our purposes) $\theta_z$ .¹z=re^{i\theta}[/latex].]

The product $zw$ two complex numbers $z$ and $w$ has absolute value equal to the product of the absolute values of $z$ and $w$ , and argument equal to the sum of the arguments of $z$ and $w$ . Symbolically, $|zw| = |z|\times|w|$ and $\theta_{zw} = \theta_z + \theta_w$ .²r_1e^{i\theta_1}\times r_2e^{i\theta_2} = r_1r_2e^{i(\theta_1+\theta_2)}[/latex].] Intuitively, the angle between the product $zw$ and the real axis is equal to the angle between $z$ and the real axis plus the angle between $w$ and the real axis. And the length of $zw$ is equal to the product of the lengths of $z$ and $w$ .

A transformation $T$ of the complex plane is a rule that assigns to every point $z$ in the plane a new point $T(z)$ . Our program lets us define transformations that rotate and scale the complex plane with respect to the origin. A rule is defined by $T(z)=az$ where $a$ is a fixed complex number. The multiplier $a$ is set using the GUI sliders abs and arg: $a$ is the complex number with absolute value $|a|$ and argument $\theta_a$ . The resulting transformation rotates by $\theta_a$ degrees around the origin and scales by a factor of $|a|$ , expanding if $|a|>1$ , contracting if $|a|<1$ , and doing neither if $|a|=1$ .

We haven’t so much as scratched the surface of complex arithmetic. To delve well beneath the surface, I recommend the books Visual Complex Analysis by Tristan Needham and Indra’s Pearls: The Vision of Felix Klein by David Mumford, Caroline Series, and David Wright, as well as the Coursera course Introduction to Complex Analysis by Petra Bonfert-Taylor. In particular, the next several pages of this site (forthcoming) are based on Indra’s Pearls.

Prev Next

Using complex exponentials, [latex ↩
[latex ↩

Michael Laszlo

It is not a something, but not a nothing either

Transformations of the complex plane