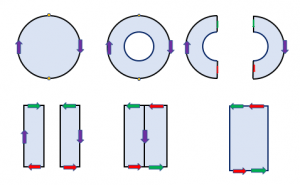
The real projective plane is obtained by gluing a disk to the boundary of a Mobius band. One way to see why: When we cut a disk out of the real projective plane, we end up with a Mobius band. In the following figure, we cut a disk out of (panel two), cut the resulting annulus along two edges while assigning red and green arrows so they remain identified (panel three), straighten the strips and glue together the purple-arrowed edges (panels four and five) to obtain the Mobius band (panel six).

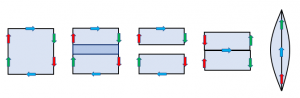
Here is another way to see that is formed by a disk glued to the boundary of a Mobius band: Cut a Mobius band out of and we’re left with a disk. In the following figure, we start with and remove one of its Mobius bands (panels one through three). Then we merge the two strips along the blue-arrowed edges (panel four), merge the pairs of red-arrowed and green-arrowed edges, and arrive at a disk (panel five).

can be immersed in 3-space in numerous interesting ways, but all of them necessarily entail self-intersection. The following program implements a standard immersion of in which we can clearly see the boundary of a disk glued to that of a Mobius band.¹

Real projective plane

To see the self-intersecting disk, select disk as the opaque surface and set opacity to zero. To recognize this as a disk, it may help to select four colors, which paints the disk’s two sides different colors. The disk intersects itself along what’s known as a double curve. Imagine cutting this disk along its double curve, from the disk’s boundary (where it appears as an X) up to the singular point. Then unfold the flaps to form a circular disk, and glue together each pair of edges. The singular point (at which the double curve terminates) maps to the center of the unfolded circular disk.

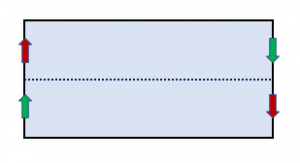
We can recognize the Mobius band similarly (select Mobius band and set opacity to zero). Imagine cutting along its double curve (where it intersects itself) up to the singular point, and then unfold the flaps. We obtain the following rectangle diagram of the Mobius band. If four colors is checked, the two colors meet along both the dotted line and the green-red arrowed edge.

In the previous two paragraphs, we imagine cutting these self-intersecting surfaces in order to bypass the resistance we expect when passing a surface through itself. But in 4-dimensional space, these surfaces need not self-intersect, and each surface can pass through itself without resistance. So we can deform instead of cut. In the ‘self-intersecting’ disk, mentally knead the double curve out until it is no longer there, yielding the familiar flat disk. In the ‘self-intersecting’ Mobius band, massage the double curve into a half-twist.