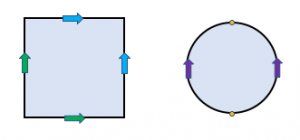
We’ve used squares with directed edges to model several surfaces. By identifying pairs of edges, the square defines other surfaces. To model the sphere (left), we glue the pair of green edges together and the pair of blue edges together. This effectively zips half the boundary to the other half in the same direction. For the sphere, a disk-based model also works (right). Each green-blue edge sequence corresponds to a purple edge of the disk.

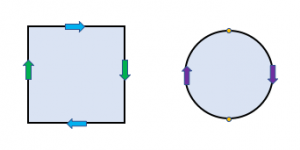
A different surface results if we direct pairs of edges in opposite directions. The resulting surface is called the real projective plane, denoted . The real projective plane can be depicted by a square-based or disk-based model.

Unlike the sphere, it’s difficult to see what looks like. It can’t be embedded in 3-space without intersecting itself. One way is to picture the disk as a hemisphere, and to identify opposite points along the hemisphere’s rim. Each rim point is glued to the point opposite it across the diameter, its so-called antipodal point. In the following program, three pairs antipodal points are highlighted in red, green, and orange. In , each pair represents a single point; for example, the two red points on the rim are merged and so represent one and the same point.

Real projective plane

In the program, let’s call the colorful semicircles ‘hemisphere lines’ since they lie on the open hemisphere. Every hemisphere line contains an antipodal pair on the rim. The families of red, green, and orange hemisphere lines are representative of all possible hemisphere lines of which there are infinitely many. In addition, a white ‘rim line’ runs along the rim. The rim line is drawn as a circle but it is actually a semicircle due to the glue operation.

In addition to lines, contains ‘points’. Every antipodal pair is a point. And the open hemisphere contains infinitely many ‘hemisphere points’.

Any two lines determine a unique point, the point at which they intersect. There are three cases: (1) Two different-colored hemisphere lines, such as a red line and orange line, intersect at a hemisphere point. (2) Two same-colored hemisphere lines intersect at the antipodal pair of the same color; for example, every pair of red lines intersect at the red antipodal point. (3) The rim line and a hemisphere line intersect at the hemisphere line’s antipodal point; for example, a green line and the white line intersect at the green antipodal point.

Just as two lines determine a unique point, any two points determines a unique line: (1) Two hemisphere points determine a hemisphere line; (2) a hemisphere point and an antipodal point determine the hemisphere line containing both points; and (3) two antipodal points determine the rim line.

The real projective plane exhibits a lovely symmetry. A line is incident with the points it contains, and a point is incident with the lines that contain it. Incidence is a symmetric relation of points and lines: Point p is incident to line l if and only if l is incident to p. As we’ve seen, every pair of lines is incident with one point and every pair of points is incident with one line. Indeed, we can swap the words ‘point’ and ‘line’ and the properties of the geometry remain the same, although this may clash with our internal picture of what points and lines ‘look like’.

In the familiar Euclidean plane, points and lines are not interchangeable. A pair of lines may or may not determine a unique point: Nonparallel lines intersect at a point whereas parallel lines do not intersect at all. In contrast, every pair of points determines a unique line.¹

The real projective plane enlarges the Euclidean plane. Starting with the points and lines of the open hemisphere, adds a ‘point at infinity’ in every direction: These are the antipodal pairs. also adds a ‘line at infinity’ containing the points at infinity: This is the white rim line. For this reason, the real projective plane is also called the extended Euclidean plane. doesn’t actually change the Euclidean plane of course, since each is a construct in its own right. But can be defined in terms of the Euclidean plane, just as the contains one, indeed many, Euclidean planes.