In plain terms, a torus is the surface of a donut.¹ More formally, a torus is a surface of revolution: Given a circle and a line that lies in the circle’s plane but does not touch the circle, revolve the circle in space around the line. This figure is called a ring torus to suggest its shape in space. They are what is produced by threejs’s TorusGeometry constructor.

A ring torus can also be constructed from a rectangular piece of very flexible material. Fold the left and right edges together and glue them to form a cylinder, and then do the same to the top and bottom edges (click the following picture to animate it).²

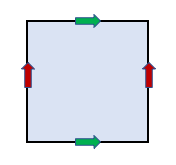
In fact, if we start with a rectangle and then conceptually, rather than physically, glue together opposite edges, we produce a flat torus. Glue together the pair of edges with red arrows (aligned in the same direction) and glue together the pair of edges with green arrows. No folding required!

The flat torus and ring torus have different geometries: the flat torus has zero curvature everywhere whereas the ring torus has plenty of curvature. But they have the same topology, that of a torus. Starting from any point p in a flat torus, if we walk left we will eventually return to point p from the right, and if we walk up we will return to point p from below. In a ring torus, these tours correspond to looping around the hole (major radius) and around the body (minor radius).³

There exist n-tori for all positive integers n where n is its dimension. A 1-torus is a circle or closed loop. Higher dimensional tori also exist but they’re harder to visualize than circles and 2-tori. ⁴

The following program depicts a flat 2-torus containing a moving shape. As the shape passes through one of the edges, it enters from the opposite edge. The entire connected shape lies inside the flat torus at all times, even though it sometimes looks like the shape splits into multiple pieces from our perspective. The torus is a closed, finite space; there’s no outside. In fact, although edges belong to a square, they do not belong to the flat torus at all. The edges are merely contraptions used to describe the space.

Flat 2-torus

When the clip checkbox is set, the scene gets clipped to the edges of the square so we see only the flat torus and the shape it contains. Clearing clip gives a look behind the scenes. It shows a group of four copies of the current shape. Whenever this group of shapes shifts too far from the square representing the flat torus, it gets translated back. This ensures that when the shape crosses some edge of the flat torus, there’s a copy of the shape in place to enter from the opposite edge.

It’s easy to imagine an ant walking on the surface of a donut suspended in space, looping any number of times around the hole and the body. But it’s harder to imagine an ant doing the same in a flat torus. We may resist the discontinuous jump that occurs when an ant crosses an edge, its splitting into pieces and coalescing into a whole. But these are only artifacts of our privileged view from outside the space. If we imagine that this flat torus is all of space, there is no discontinuity at all.