A flat 3-torus is like a flat 2-torus but one dimension higher. Start with a solid box, and then conceptually glue opposite faces.1 Since there are six faces, there are three glue operations.
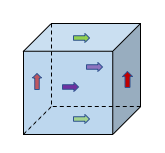
As an object exits one side of the flat torus, it enters from the opposite side. As with the flat 2-torus, only a single connected object lies in the space even though from the outside it may sometimes appear disconnected. Faces do not belong to the flat 3-torus; they’re just artifacts of the torus’s description. To emphasize this, you can check trans walls to hide the faces.
You can see how the program works by clearing the clip checkbox. It’s the same strategy we used for the flat 2-torus program only one dimension higher.
One natural embedding of the 2-torus in 3-dimensional space is of course the ring torus. This gives us a way of viewing the 2-torus from outside so to speak. But it’s not possible to embed the 3-torus in 3-dimensional space unless we allow it to intersect itself. This would require 4-dimensional space. We’ll look at ways of seeing the 3-torus from the outside later. But it’s not hard to see what it looks like from the inside, which we do on the next page.
- Each point of a face gets glued to the point directly opposite it so that face pairs are glued without twisting them. ↩