Circle inversions

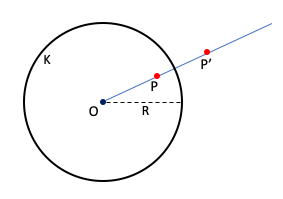
We explore reflection in a circle. Let $K$ be a circle with center $O$ and radius $R$ . We call $K$ the inversion circle. Every point $P$ in the plane reflects to a point $P'$ across the inversion circle. The rule is that $P'$ is the unique point on the ray from $K$ ‘s center $O$ through $P$ such that $OP\cdot OP'=R^2$ .

A few things of note. Reflection is its own inverse, meaning that reflecting a point twice yields that same point. Points that lie on circle $K$ reflect to themselves. Points in the interior of $K$ (other than its center $O$ ) reflect to points in its exterior, and points in $K$ ‘s exterior reflect to points in its interior.

Since center $O$ of circle $K$ lies at distance 0 from itself, its reflection is at infinity. To allow for this, the plane is extended with a single point $\infty$ at infinity. Now, $O$ reflects to $\infty$ and $\infty$ reflects to $O$ .

We’ve looked at the reflection of points in the inversion circle $K$ , but in fact we can reflect any geometric figure — any set of points — in $K$ . The reflection of a figure is the set of reflections of the points that comprise it. Suppose, for example, the figure is a circle. The reflection of a circle $C$ not containing $K$ ‘s center $O$ is another circle. If circle $C$ does contain $O$ , its reflection is a line.¹ Accordingly, we broaden our definition of “circle” to include both circles and lines by regarding a line as a circle of infinite radius, in other words, a line is a circle that contains the point $\infty$ . Then it becomes fair to say that the reflection of every circle is a circle.

The following program illustrates reflection of a disk in the inversion circle $K$ indicated by the thin red cylinder. The disk $D$ is light gray and its reflection $D'$ is blue. When you drag $D$ to a new position, its reflection updates when you release. You can change $D$ ‘s radius using the GUI slider.

Disk inversions

The shape of disk $D$ ‘s reflection depends on whether it contains the center $O$ of inversion circle $K$ . When $O$ lies in $D$ ‘s exterior, $D$ ‘s reflection is a disk in the plane. In contrast, when $O$ lies in $D$ ‘s interior, its reflection is a disk that contains $\infty$ . We render this as an annulus (ring) with the understanding that its outer boundary closes on itself at infinity. Lastly, when $O$ lies on $D$ ‘s boundary, $D$ ‘s reflection is a half-plane whose boundary is a line. Since this half-plane includes the point $\infty$ , it too is actually a disk. Just as circles, broadly defined, reflect to circles, disks reflect to disks.

Prev Next

Since the reflection of $O$ is $\infty$ , if we assume $O\in C$ , $C$ ‘s reflection contains $\infty$ making it a circle of infinite radius, that is, a line. ↩

Michael Laszlo

It is not a something, but not a nothing either

Circle inversions