Walk into splintered sunlight
Inch your way through dead dreams to another land
— Box of Rain, Grateful Dead

Suppose we start with three non-overlapping disks, each tangent to the other two. These are the three blue disks in the following figure.¹ The two ‘smaller’ blue disks render as conventional disks whereas the third appears as a blue ring: This disk contains the point at infinity. We can think of these three disks as lying in a common sphere.

Next, we remove the three blue disks, which leaves behind two red ideal triangles whose sides meet at zero degrees at the vertices. Next, inscribe a yellow disk in each of the two red triangles. When we remove each yellow disk, three smaller red ideal triangles remain.

The process proceeds indefinitely: we inscribe a disk in each ideal triangle, thereby partitioning it into three smaller ideal triangles. The following figure follows the process for two more steps, yielding the green circles and then the purple circles.

As the process continues, we approach the limit set known as the Apollonian gasket, the set of ‘red’ points that remain when all inscribed circles have been removed. It’s what the red ideal triangles ultimately shrink to. In the following figure, the Apollonian gasket is approximated by the black curve.

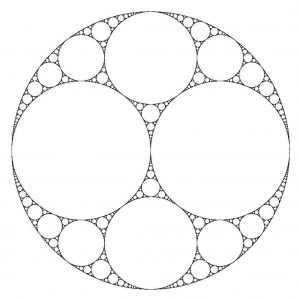
Remarkably, the Apollonian gasket also arises under Schottky dynamics.² Not only are the four seed disks tangent in a chain, but paired disks are also tangent: to , and to . In the following program, set nbrLevels to 0 and model to ‘disks’. Three of the seed disks appear as disks, and the fourth disk’s boundary is indicated by the red line.³ Note that each of the disks is tangent to the other three.

Mutual tangencies propagate throughout the gasket. At every level, each disk contains three smaller disks that are tangent to one another and to itself. One way to see this is to increase nbrLevels and set model to ‘disks’ and color model to ‘by level’. Choose some disk and observe how the three disks it contains at the next level are pairwise tangent. Next, click on some deepest disk to see how it expands into its pairwise tangent children. As you repeatedly click to expand, two chains of disks emerge which gradually converge to a point of tangency.