As we’ve seen, the dynamics of a loxodromic transformation cause circles and points to spiral out from the origin (source) toward infinity (sink). But since infinity is just another point in the extended complex plane, any pair of points can serve as source and sink. In the following program, the points -1 and 1 are source and sink respectively.
The following figures from Indra’s Pearls1 illustrate the difference between the previous page’s program and the present one. The south pole of the Riemann sphere sits at the origin of the extended complex plane, and stereographic projection maps the sphere to the plane. The sphere’s south pole projects to the origin and the north pole to infinity; green lines of latitude project to circles concentric on the origin, and yellow lines of longitude to rays emanating from the origin. The red spiral from the south pole to the north pole projects to a spiral from the origin to infinity in the extended complex plane.
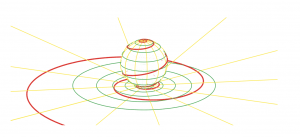
In the next figure, the Riemann sphere is rotated 90° so that, under stereographic projection, points spiral from -1 to 1. This is what the program on this page implements. Spirals in the two figures (and in the two programs) are the same up to rotation of the Riemann sphere.
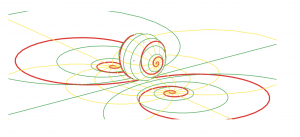
- Indra’s Pearls, Chapter 3, Figures 3.1 and 3.4. ↩