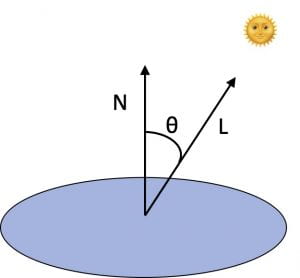
Flat shading renders each face in a single color, without varying the color across the face. This color is obtained from a single lighting calculation on each face. Typically, this calculation uses the face’s orientation relative to the light sources to determine how much energy illuminates the face, which in turn determines the brightness level of the face’s color. Orientation is represented by a normal vector to the face. The energy contributed by a light source is approximated by where is the angle between the normal vector to the face and the vector pointing to the light source. Since the same shade is applied uniformly across the face, it appears flat.

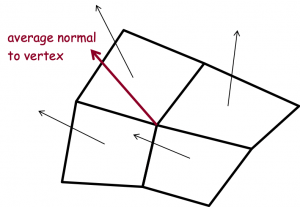
A smooth shading model makes a lighting calculation at ever vertex of a face, and then interpolates the vertices’ colors across the interior of the face. Typically, the normal to each vertex is used to calculate each vertex’s color. Since surfaces usually change orientation at vertices, it’s sensible to ask, What is the surface normal at a vertex? Assume the faces are embedded in a mesh (such as a face of a sphere or torus) so that there are multiple faces encircling each vertex. Each vertex normal depends on the orientation of the faces that encircle it: It is the average of the faces’ surface normals. So we assign the average normal to each vertex, and then apply the lighting model to obtain the vertex’s color. Each face is painted by interpolating the colors of its vertices, giving the impression of curvature across the face.

The blue square in the following program is not embedded in a larger mesh, so there are no natural average normals at its four vertices. Rather, we determine their normals, depicted by the red line segments, using the GUI slider. The value is the angle (in degrees) between the normals and the vertical y-axis. Positive values generate outward-pointing normals, and negative values inward-pointing normals. Notice how the square’s apparent curvature is affected by change in these normal vectors, even though the square remains geometrically flat. As the normals vary, the shades associated with their vertices vary and these shades are interpolated across the square’s interior. ¹

Some shading models

Here are two experiments using Lambert shading. First, place the light source along the vertical y-axis. When the vertex normals point toward the light source the square is brightly illuminated, when they point away, it is only dimly illuminated. Second, place the light source beyond one of the square’s corners. Only the corner whose normal points toward the light gets brightly lit.²

We smooth-shade a mesh by assigning it a MeshLambertMaterial. A surface is called Lambertian if its brightness does not depend on the viewer’s position (though it does depend on the position of light sources). You can see this is true of the scene when Lambert is selected. The technique to achieve this, based on performing a lighting calculation on the vertices’ average normals and then interpolating colors, is called Gouraud shading. MeshLambertMaterial uses Gouraud shading. In contrast, we get no shading, menu item none, by assigning the MeshBasicMaterial to the mesh.