Lighting models

As we’ve seen, a shading model performs select lighting calculations to shade facets. For example, Lambert shading performs lighting calculations at the vertices and then interpolates colors across facet interiors. Phong shading performs a lighting calculation at every fragment of a facet. Whatever the shading model, the lighting calculation applies some lighting model.

A lighting calculation may take into account both local and global factors. Local factors include surface geometry and material, and surface orientation with respect to light sources and the viewer. In contrast, global factors account for interaction of light between objects in the scene graph: reflection and refraction between objects, casting of shadows, lensing effects, and the like. Accounting for global factors is computationally expensive, so real-time systems like three.js provide limited support for them ¹. Here here we’ll consider a standard lighting model that accounts only for local factors.

Light strikes a surface and, through reflection, illuminates the surface. If the surface is rough, the reflected light scatters in all directions. If the surface is smooth, the reflected light is fairly focused in a certain direction. Surfaces such as dirt and carpets are very rough, and surfaces such as mirrors, water, and polished metals are very smooth, but most surfaces are a blend of rough and smooth. Here, ‘rough’ and ‘smooth’ refer to a surface’s features at microscopic level at which it interacts with light, which roughly correlates with the surface finish we see.

Diffuse reflection is reflection due to a material’s roughness. When we refer to the color of an object — brown wood, green grass, blue sky — we’re talking about its diffuse color. The amount of light a surface reflects diffusely depends on how much light energy falls on the surface. We break light into two components:

Ambient light, which has neither source nor direction, just fills space with a uniform intensity. There is ambient light at Earth’s surface because our atmosphere scatters light, whereas there’s no ambient light in outer space since there’s no atmosphere to scatter light.

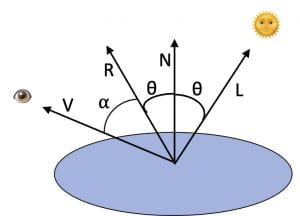
Diffuse light strikes a surface from a certain direction. The amount of diffuse light that strikes a surface depends on its orientation to the light source: A lot of light if the light illuminates the surface from above, but little light if it just grazes the surface from an oblique angle. Surface orientation with respect to the light source is represented by the angle $\theta$ between the normal vector $N$ to the surface and the light vector $L$ that points to the light source. The amount of diffuse light that strikes the surface is approximated by $\cos\theta$ . When $\theta$ is close to zero (the light source is overhead), $\cos\theta\approx1$ ; and when $\theta$ is close to $\pi/2$ (the light grazes the surface), $\cos\theta\approx0$ .

We’ll let $I_a$ denote the intensity of ambient light and $I_d$ the intensity of the diffuse light. We’ll also let $k_a$ denote the percentage of ambient light reflected by the surface, and $k_d$ the percentage of diffuse light reflected by the surface. ( $k_a$ and $k_d$ are called ambient and diffuse reflection coefficients respectively.) Then the intensity of light reflected due to surface roughness (scattering in all directions) is given by

$k_a I_a + k_d I_L \cos\theta$

Where the $N$ and $L$ are unit vectors (i.e., of length one), we have $\cos\theta=N\cdot L$ , so this simplifies to²

$k_a I_a + k_d I_L (N\cdot L)$

We turn to the intensity contribution due to specular reflection, that is, due to a material’s smoothness. This reflection appears as a shiny spot, or specular highlight, that reflects into eye. To account for specular reflection, the orientation of the surface with respect to the viewer’s position comes into play. Let $R$ be the reflection vector, the direction in which the light would be reflected if the surface were a perfect mirror. And let $V$ be the vector toward the viewer. The angle $\alpha$ between $R$ and $V$ quantifies how far the viewer is from the center axis of specular highlight. We approximate the amount of specular light that the eye sees by $(\cos\alpha)^s$ where $s$ is the shininess exponent. The specular highlight is increasingly tight and well-defined with higher values of $s$ : A rough surface is modeled by $s=1$ whereas the surface becomes more mirrorlike as $s$ increases.

Let $k_s$ be the specular reflection coefficient for the material. Then the intensity contribution due to specular reflection is given by

$k_s I_L (R\cdot V)^s$

Combining diffuse and specular contributions over multiple light sources $L$ yields the following equation for intensity at a point of a surface:

$I = k_a I_a + \sum_L(k_d I_L (N\cdot L) + k_s I_L (R\cdot V)^s)$

The following program can be used to experiment with this lighting model. Both surfaces are assigned the MeshPhongMaterial.

Lighting model

The ambient light and spotlight both cast white light whose brightness you can adjust with the two intensity sliders. The diffuse color selector sets both the ambient and diffuse reflection coefficient. In effect, it controls the fraction of reflected light in the color components red, green, and blue. The specular color selector is used similarly to set the specular coefficient in each of the color components. Shininess controls the shininess exponent.

Prev Next

Ray tracing and radiosity are two standard methods that account for global, inter-object lighting effects. ↩
Here $N\cdot L$ is the dot product of these two unit vectors. In practice, intensity is nonnegative, so we write $N\cdot L$ as shorthand for $\max\lbrace0, N\cdot L\rbrace$ . ↩

Michael Laszlo

It is not a something, but not a nothing either

Lighting models