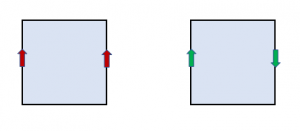
As we’ve seen, we can construct a cylinder from a filled square by gluing together left and right edges. A Möbius band is also constructed by gluing together left and right edges, but they get glued with a flip. Here is the plan for the cylinder (left) and the Möbius band (right).
When a two-dimensional figure living in a Möbius band crosses the right edge, it comes back the opposite edge mirror reversed. In the following program, the face’s left eye is red. But after crossing the edge once, its right eye is now red. The figure returns in its mirror image. One more crossing and its left eye is once again red. Each loop along the length of the Möbius band flips the figure’s orientation.1
A surface that contains a path that reverses orientation is called nonorientable, whereas a surface in which every path preserves orientation is called orientable. Möbius bands are nonorientable, whereas cylinders, spheres, and tori are orientable.
Clear the clip checkbox to see how the program works.
- Imagine you are a two-dimensional, right-handed individual living in a Möbius band. When you travel once along the band’s length and arrive back at your starting point, you find yourself left handed. Loop around once again and you’re back to being right handed. Remarkable! Though perhaps not as remarkable as discovering that you’re a two-dimensional creature living in a Möbius band. ↩