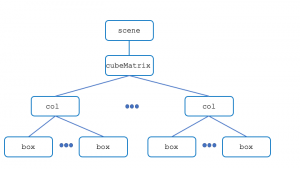
There are many ways to skin a cat. (We’re best advised to take this euphemism euphemistically rather than literally.) The scene graph for the 2D matrix of cubes of the previous page is very shallow: All m×n cubes are children of a common parent node. Another possible scene graph consists of a row of columns. Here, we construct a column of cubes parallel to the vertical y-axis, and then translate instances of these columns horizontally along the x-axis. Here is code for constructing such as scene graph.

function createCubeMatrix(m, n, offset) {
    let root = new THREE.Object3D();
    offset = offset !== undefined ? offset : 2.0;
    let geom = new THREE.CubeGeometry(1, 1, 1);
    let mat = new THREE.MeshLambertMaterial({transparent: true})
    let xMin = -offset * ((m-1) / 2.0);
    let yMin = -offset * ((n-1) / 2.0);
    for (let i = 0, x = xMin; i < m; i++, x += offset) {
        let col = new THREE.Object3D()
        for (let j = 0, y = yMin; j < n; j++, y += offset) {
            let box = new THREE.Mesh(geom, mat);
            box.position.y = y;
            col.add(box);
        }
        col.position.x = x;
        root.add(col);
    }
    return root;
}

This is what this scene graph looks like. Each column col has its own x position.

Once we have a 2D slab of cubes, it’s not difficult to build a 3D block of cubes. One way is to add m×n×p cubes to a common parent node, generalizing the scene graph of the previous page. Alternatively, we could construct a 2D slab of m×n cubes in the xy-plane, and then translate p instances of this slab in the perpendicular direction, that is, along the z-axis, generalizing the current scene graph. And there are still other ways to skin this cat. Give it some thought.

I could not resist allowing selection of geometries other than boxes in the following program. It’s not hard to define any sort of object and pass it as an argument to createCubeMatrix, instead of hard-coding construction of boxes inside this function.

Block of cubes and other things