Here we start with a polyhedron, and then recursively project a scaled copy through each of its vertices. In the following 2D version, the black-outlined polygon gets projected through its vertex to yield the scaled-down red polygon.

In same fashion, the black polygon would be projected through its three other vertices to yield a total of four scaled copies of itself, each connected to one of its vertices. The same process is applied to the four scaled-down polygons down to any number of levels.

Corner connected fractals

The following function gets called with the number of levels, the base geometry geom, and the scale factor. It first builds a mesh base on the geometry. To build a scaled geometry at the next level, geom gets projected across each of its vertices : Every vertex of geom projects to the vertex where is the scale factor. Note that the vertices of the new geometry are loaded into a clone of the original geometry geom. This is done to connect the original geometry’s faces to the new array of vertices.

function makeCornerConnected(level, geom, scale, stopvertex=null) {
    let base = new THREE.Mesh(geom, materials[level]);
    if (level > 0) {
        let vertices = geom.vertices;     
        for (let v of vertices) {
            if (stopvertex && v.equals(stopvertex))
                continue;
            let newGeom = geom.clone();
            // add vertices to new geometry: v + scale * (v - w)
            newGeom.vertices.length = 0;
            for (let w of vertices) {
                let wp = v.clone();
                wp.sub(w);
                wp.multiplyScalar(scale);
                wp.add(v);
                newGeom.vertices.push(wp);
            }
            let newFractal = makeCornerConnected(level-1, newGeom, scale, v);
            base.add(newFractal);
        }   
    }
    return base;
}

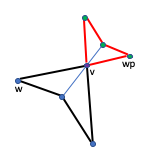
The stopvertex parameter prevents ‘back projection’. In the previous figure, if we were to project the red polygon across vertex to produce an even smaller blue polygon, the blue polygon would be enclosed inside the black polygon. Generating the red polygon with stopvertex equal to prevents generation of the blue polygon.

In the program, you can choose the base geometry from several convex polyhedra. Click the Stellate button to translate some of the base geometry’s vertices toward or away from the center, resulting in a less symmetrical polyhedron that need not be convex.

The facets comprising each level’s polyhedra are oriented reverse those of the parent’s level. If mesh sidedness is set to DoubleSide, the polyhedra at every level are rendered as solids. However, if sidedness is set to FrontSide, only those polyhedra at even levels are rendered as solids, whereas back-facing facets of odd-level polyhedra are discarded. You can see the effect by toggling the frontSided checkbox.